Downlaod (![]() ) Click here Pages: 3, Size: 38.40 KB, Filetype: pdf
) Click here Pages: 3, Size: 38.40 KB, Filetype: pdf
|
No. |
Question |
Click here to see answers |
|
1 |
A man whirls a stone of mass 250 gram, tied at the end of a string of length 2 m in a horizontal circle and at a height of 5 m from the ground. The string breaks and the stone flies off tangenitially and strikes the ground at a horizontal distance of 10 m from the man. What was the magnitude of the centripetal acceleration of the stone, when it was moving in the circle? (g = 10 m/s2) (a) 50 m/s2 (b) 40 m/s2 (c) 30 m/s2 (d) 25 m/s2 |
|
|
2 |
A mass of 5 kg is tied to a string of length 1.0 m and is rotated in vertical circle with a uniform speed of 4 m/s. The tension in the string will be 130 N when the mass is at (g = 10 m/s2) (a) highest point (b) mid way (c) bottom (d) cannot be justified |
|
|
3 |
A mass suspended on a frictional less horizontal surface. It is attached to a string and rotates about a fixed centre at an angular velocity w0. If length of the string and angular velocity are doubled the tension in the string which was initially T0 is now (a) T0 (b) (c) 4 T0 (d) 8 T0 |
|
|
4 |
A metal sphere of mass 0.1 kg is attached to an inextensible string of length 130 cm whose upper end is fixed to the rigid support. If the sphere is made to describe a horizontal circle of radius 50 cm, the time for its one revolution is near (a) 1.2 sec (b) 2.2 sec (c) 1.5 sec (d) 3 sec |
|
|
5 |
A motor cyclist loops a vertical circular loop of diameter 18 m, without dropping down, even at the highest point of the loop. What should be his minimum speed at the lowest point of the loop? (a) 10 m/s (b) 16 m/s (c) 21 m/s (d) 30 m/s |
|
|
6 |
A motor cyclist moving with a velocity of 75 km/hr on a flat road takes a turn on the road at a point where the radius of curvature of the road is 20 m. If the g is 10 m/s2 the maximum angle of banking with vertical for no skidding is (a) tan–1 (6) (b) tan–1 (2) (c) tan–1 (12) (d) tan–1 (4) |
|
|
7 |
A particle is acted upon by a force of constant magnitude which is always perpendicular to the velocity of the particle. The motion takes place in a plane. It follows that (a) its velocity is constant (b) its acceleration is constant (c) its motion is linear (d) its motion is circular |
|
|
8 |
A particle is moving along a circular path. Let v, w, a and ac be its linear velocity, angular velocity, angular acceleration and centripetal acceleration respectively. Which is the wrong statement from the followings? (a) (b) (c) (d) |
|
|
9 |
A particle is performing a U.C.M. Which is the wrong statement regarding its motion? (a) The velocity vector is tangential to the circle (b) The acceleration vector is tangential to the circle (c) The acceleration vector is directed towards the centre of the circle (d) The velocity and acceleration vectors are perpendicular to each other |
|
|
10 |
A particle is performing U.C.M. along a circular path of radius r, with a uniform speed v. Its tangential and radial acceleration are (a) zero and infinite (b) (c) zero and (d) rw2 and infinite |
|
|
11 |
A particle moves in a circular path of radius r, in half of its period. Its displacement and distance covered are, (a) 2r, 2pr (b) r (c) 2r, pr (d) r, pr |
|
|
12 |
A particle moving in a circle of radius 25 cm at 2 revolutions per second. The acceleration of the particle is S.I. unit is (a) 4p2 (b) 3p2 (c) 2p2 (d) p2 |
|
|
13 |
A particle of mass ‘m’ moves with a constant speed along a circular path of radius r under the action of a force F. Its speed is given by (a) (b) (c) (d) |
|
|
14 |
A particle of mass m is executing uniform circular motion on a path of radius r. If P is the magnitude of its linear momentum, then, the radial force acting on the particle is, (a) pmr (b) (c) (d) |
|
|
15 |
A particle of mass m is moving in a horizontal circle of radius R with uniform speed v. When it moves from one point to a diametrically opposite point its (a) kinetic energy changes by Mv2/4 (b) momentum does not change (c) momentum changes by 2 Mv2 (d) kinetic energy changes by Mv2 |
|
|
16 |
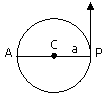
A particle P is moving in a circle of radius ‘a’ with uniform speed v. C is the centre of the circle and AP is diameter. The angular velocity of P about A and C are in the ratio (a) 1 : 1 (b) 1 : 2 (c) 2 : 1 (d) 4 : 1 |
|
|
17 |
A particle rests on the top of a hemisphere of radius R. The smallest horizontal velocity that must be imparted to the particle if it is to leave the hemisphere without sliding down is (a) (b) (c) (d) |
|
|
18 |
A particle revolves round a circular path. The acceleration of the particle is (a) along the circumference of the circle (b) along the tangent (c) along the radius (d) zero |
|
|
19 |
A person with his hands in his pocket is skating on ice at the rate of 10 m/s and describes a circle of radius 50 m. What is his inclination to the vertical? (g = 10 m/s2) (a) tan–1 (b) tan–1 (c) tan–1 (d) tan–1 |
|
|
20 |
A pulley one metre in diameter rotating at 600 r.p.m. is brought to rest in 80 sec. by a constant force of friction on its shaft. How many revolutions does it makes before coming to rest? (a) 200 (b) nbsp; 300 (c) 400 (d) 500 |
|
|
21 |
A satellite has mass m speed v and radius r, the force acting on it is: (a) zero (b) mrv2 (c) (d) |
|
|
22 |
A simple pendulum of effective length ‘l’ is kept in equilibrium in vertical position. What horizontal velocity should be given to its bob, so that it just completes a vertical circular motion? (a) (b) (c) (d) |
|
|
23 |
A simple pendulum of mass m and length l stands in equilibrium in vertical position. The maximum horizontal velocity that should be given to the bob at the bottom so that it completes on revolution is (a) (b) (c) (d) |
|
|
24 |
A small body attached at the end of an inextensible string completes a vertical circle, then its (a) angular velocity remains constant (b) angular momentum remains constant (c) total mechanical energy remains constant (d) linear momentum remains constant |
|
|
25 |
A small body is to be moved inside a vertical circular tube of radius l. What minimum velocity should be imparted to it, as its lowest point so that it can just complete the vertical circle? (a) (b) (c) (d) |
|
Answers to Circular Motion, Paper 2
| 1. Ans.: a | 2. Ans.: c | 3. Ans.: d | 4. Ans.: b | 5. Ans.: c |
| 6. Ans.: b | 7. Ans.: d | 8. Ans.: c | 9. Ans.: b | 10. Ans.: c |
| 11. Ans.: c | 12. Ans.: a | 13. Ans.: a | 14. Ans.: d | 15. Ans.: b |
| 16. Ans.: b | 17. Ans.: a | 18. Ans.: c | 19. Ans.: b | 20. Ans.: c |
| 21. Ans.: d | 22. Ans.: a | 23. Ans.: d | 24. Ans.: c | 25. Ans.: d |