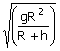Downlaod (![]() ) Click here Pages: 2, Size: 36.18 KB, Filetype: pdf
) Click here Pages: 2, Size: 36.18 KB, Filetype: pdf
|
Scroll down to the end of page to see answers.
|
|
|
1. |
A satellite is revolving around the sun in a circular orbit with uniform velocity v. If the gravitational force suddenly disappears, the velocity of the satellite will be (a) zero (b) v (c) 2v (d) infinity |
|
2. |
Who among the following first gave the experimental velocity of G? (a) Cavendish (b) Copernicus (c) Brook Taylor (d) none of these |
|
3. |
The mean radius of the earth is R, its angular speed on its own axis is ω and the acceleration due to gravity at earth’s surface is g. The cube of the radius of the orbit of a geo-stationary satellite will be (a) r2g/ ω (b) R2ω2 / g (c) RG ω2 (d) R2g/ ω2 |
|
4. |
The largest and the shortest distance of the earth from are r1 and r2. It’s distance from the sun when it is perpendicular to the major-axis of the orbit drawn from the sun. (a) (b) (c) (d) |
|
5. |
Geo-stationary satellite (a) revolves about the polar axis (b) has a time period less than that of the earth’s satellite (c) moves faster than a near earth satellite (d) is stationary in the space |
|
6. |
A spherical planet far out in space has a mass M0 and diameter D0. A particle of mass m falling freely near the surface of this planet will experience an acceleration due to gravity which is equal to (a) (b) (c) (d) |
|
7. |
Two planets of radii r1 and r2 are made from the same material. The ratio of the acceleration due to gravity g1/g2 at the (a) (b) (c) (d) |
|
8. |
If g is the acceleration due to gravity of the earth’s surface the gain in the potential energy of an object of mass m raised from the surface of the earth to a height equal to the radius R of the earth is (a) (b) 2mgR (c) mgR (d) |
|
9. |
An earth’s satellite of mass m revolves in a circular orbit at a height h from the surface g is acceleration due to gravity at the surface of the earth. The velocity of the satellite in the orbit is given by (a) (b) gR (c) (d) |
|
10. |
If the radius of the earth were to shrink by one percent, its mass remaining the same, the acceleration due to gravity on the earth’s surface would (a) decrease (b) remains unchanged (c) increase (d) none of these |
|
11. |
The escape velocity from the earth’s surface is 11 km/sec. A certain planet has a radius twice that of the earth but its mean density is the same as that of the earth. The value of the escape velocity from this planet would be (a) 22 km/sec (b) 11 km/sec (c) 5.5 km/sec (d) 16.5 km/sec |
|
12. |
The escape velocity from earth is 11.2 km per sec. If a body is to be projected in a direction making an angle 45° to the (a) 11.2 × 2 km/sec (b) 11.2 km/sec (c) 11.2 × (d) 11.2 × |
|
13. |
What would be the duration of the year if the distance between the earth and the sun gets doubled? (a) 1032 days (b) 129 days (c) 365 days (d) 730 days |
|
14. |
If escape velocity from the earth’s surface is 11.2 km/sec. then escape velocity from a planet of mass same as that of earth but radius one fourth as that of earth is (a) 11.2 km/sec (b) 22.4 km/sec (c) 5.65 km/sec (d) 44.8 km/sec |
|
15. |
A thin uniform, circular ring is rolling down an inclined plane of inclination 30° without slipping. Its linear acceleration (a) g/2 (b) g/3 (c) g/4 (d) 2g/3 |
|
16. |
A artificial satellite moving in a circular orbit around the earth has a total (kinetic + potential) energy E0. Its potential energy is (a) 2E0 (b) E0 (c) 1.5 E0 (d) –E0 |
|
17. |
The distance between centre of the earth and moon is 384000 km. If the mass of the earth (a) 1 km/sec (b) 4 km/sec (c) 8 km/sec (d) 11.2 km/sec |
|
18. |
When body is raised to a height equal to radius of earth, the P.E. change is (a) MgR (b) (c) 2 MgR (d) none of these |
|
19. |
A planet has twice the radius but the mean density is 1/4th as compared to earth. What is the radio of the escape velocity from the earth to that from the planet? (a) 3 : 1 (b) 1 : 2 (c) 1 : 1 (d) 2 : 1 |
|
20. |
The masses of two planets are in the ratio 1 : 2. Their radii are in the ratio 1 : 2. The acceleration due to gravity on the planets are in the ratio. (a) 1 : 2 (b) 2 : 1 (c) 3 : 5 (d) 5 : 3 |
|
21. |
If the acceleration due to gravity of a planet is half the acceleration due to gravity of earth’s surface and radius of planet is half the radius of the earth, the mass of planet in terms of mass of earth is (a) (b) (c) (d) |
|
22. |
The radii of the earth and the moon are in the ratio 10 : 1 while acceleration due to gravity on the earth’s surface and moon’s surface are in the ratio 6 : 1. The ratio of escape velocities from earth’s surface to that of moon surface is (a) 10 : 1 (b) 6 : 1 (c) 1.66 : 1 (d) 7.74 : 1 |
|
23. |
Acceleration due to gravity g in terms of mean density of Earth d (where R is radius of earth and G – universal gravitational constant) is (a) g = 4πR2 d G (b) g = (c) g = (d) g = |
|
24. |
The dimensions of universal gravitational constant are (a) M2 L2 T–2 (b) M–1 L3 T–2 (c) M L–1 T–2 (d) M L2 T–2 |
|
25. |
If R is radius of the earth and g the acceleration due to gravity on the earth’s surface, the mean density of the earth is (a) (b) (c) (d) |
Answers to Gravitation, Paper 2
| 1. Ans.: (b) | 6. Ans.: (c) | 11. Ans.: (a) | 16. Ans.: (a) | 21. Ans.: (d) |
| 2. Ans.: (a) | 7. Ans.: (a) | 12. Ans.: (b) | 17. Ans.: (a) | 22. Ans.: (d) |
| 3. Ans.: (d) | 8. Ans.: (a) | 13. Ans.: (a) | 18. Ans.: (b) | 23. Ans.: (d) |
| 4. Ans.: (c) | 9. Ans.: (d) | 14. Ans.: (b) | 19. Ans.: (c) | 24. Ans.: (b) |
| 5. Ans.: (a) | 10. Ans.: (c) | 15. Ans.: (c) | 20. Ans.: (a) | 25. Ans.: (c) |